Биноминальное распределение

В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель - это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения.

Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.

Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.

Выборка состоит из фиксированного числа элементов n , представляющих собой исходы некоего испытания.
Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача.
Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 – р .
Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.

Скачать заметку в формате или , примеры в формате

Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.

Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n .

Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:

Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:

Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009. Если же необходимо вычислить количество вариантов выбора X n элементов, следует воспользоваться формулой сочетаний (1):

где n! = n * (n –1) * (n – 2) * … * 2 * 1 - факториал числа n , причем 0! = 1 и 1! = 1 по определению.

Это выражение часто обозначают как . Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:

Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:

(Количество возможных последовательностей) *
(вероятность конкретной последовательности) = 4 * 0,0009 = 0,0036

Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.

Биноминальное распределение

где Р(Х) - вероятность X успехов при заданных объеме выборки n и вероятности успеха р , X = 0, 1, … n .

Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X , подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n . Произведение р X (1 – р) n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n . Величина определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях. Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна

Р(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =

Рассмотрим примеры, иллюстрирующие применение формулы (2).

1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна

2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна

Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна

Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037

3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события

Р(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)

Используя формулу (2), вычислим каждую из этих вероятностей:

Следовательно, Р(Х < 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.

Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.

По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее. Некоторые из этих вероятностей приведены рис. 1. Например, чтобы получить вероятность, что Х = 2 при n = 4 и p = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0,1.

Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1

Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х , число испытаний (или объем выборки) – n , вероятность успеха – р , параметр интегральная , принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).

Рис. 2. Параметры функции =БИНОМ.РАСП()

Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле. Цифрами показаны ответы на примеры соответствующего номера).

Рис. 3. Расчет биноминального распределения в Excel для n = 4 и p = 0,1

Свойства биномиального распределения

Биномиальное распределение зависит от параметров n и р . Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,05, биномиальное распределение является симметричным независимо от величины параметра n . Однако, если р ≠ 0,05, распределение становится асимметричным. Чем ближе значение параметра р к 0,05 и чем больше объем выборки n , тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).

Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1

Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р :

(3) Μ = Е(Х) = np

В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.

Стандартное отклонение биномиального распределения

Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:

Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313

Биномиальное распределение - одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины. Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях . Часто событие А называют "успехом" наблюдения, а противоположное ему событие - "неуспехом", но это обозначение весьма условное.

Условия биномиального распределения :

в общей сложности проведено n испытаний, в которых событие А может наступить или не наступить;
событие А в каждом из испытаний может наступить с одной и той же вероятностью p ;
испытания являются взаимно независимыми.

Вероятность того, что в n испытаниях событие А наступит именно m раз, можно вычислить по формуле Бернулли:

где p - вероятность наступления события А ;

q = 1 - p - вероятность наступления противоположного события .

Разберёмся, почему биномиальное распределение описанным выше образом связано с формулой Бернулли . Событие - число успехов при n испытаниях распадается на ряд вариантов, в каждом из которых успех достигается в m испытаниях, а неуспех - в n - m испытаниях. Рассмотрим один из таких вариантов - B 1 . По правилу сложения вероятностей умножаем вероятности противоположных событий:

а если обозначим q = 1 - p , то

Такую же вероятность будет иметь любой другой вариант, в котором m успехов и n - m неуспехов. Число таких вариантов равно - числу способов, которыми можно из n испытаний получить m успехов.

Сумма вероятностей всех m чисел наступления события А (чисел от 0 до n ) равна единице:

где каждое слагаемое представляет собой слагаемое бинома Ньютона. Поэтому рассматриваемое распределение и называется биномиальным распределением.

На практике часто необходимо вычислять вероятности "не более m успехов в n испытаниях" или "не менее m успехов в n испытаниях". Для этого используются следующие формулы.

Интегральную функцию, то есть вероятность F (m ) того, что в n наблюдениях событие А наступит не более m раз , можно вычислить по формуле:

В свою очередь вероятность F (≥m ) того, что в n наблюдениях событие А наступит не менее m раз , вычисляется по формуле:

Иногда бывает удобнее вычислять вероятность того, что в n наблюдениях событие А наступит не более m раз, через вероятность противоположного события:

Какой из формул пользоваться, зависит от того, в какой из них сумма содержит меньше слагаемых.

Характеристики биномиального распределения вычисляются по следующим формулам .

Математическое ожидание: .

Дисперсия: .

Среднеквадратичное отклонение: .

Биномиальное распределение и расчёты в MS Excel

Вероятность биномиального распределения P n (m ) и значения интегральной функции F (m ) можно вычислить при помощи функции MS Excel БИНОМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:

число успехов;
число испытаний;
вероятность успеха;
интегральная - логическое значение: 0 - если нужно вычислить вероятность P n (m ) и 1 - если вероятность F (m ).

Пример 1. Менеджер фирмы обобщил информацию о числе проданных в течение последних 100 дней фотокамер. В таблице обобщена информация и рассчитаны вероятности того, что в день будет продано определённое число фотокамер.

День завершён с прибылью, если продано 13 или более фотокамер. Вероятность, что день будет отработан с прибылью:

Вероятность того, что день будет отработан без прибыли:

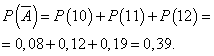
Пусть вероятность того, что день отработан с прибылью, является постоянной и равна 0,61, и число проданных в день фотокамер не зависит от дня. Тогда можно использовать биномиальное распределение, где событие А - день будет отработан с прибылью, - без прибыли.

Вероятность того, что из 6 дней все будут отработаны с прибылью:

Тот же результат получим, используя функцию MS Excel БИНОМ.РАСП (значение интегральной величины - 0):

P 6 (6 ) = БИНОМ.РАСП(6; 6; 0,61; 0) = 0,052.

Вероятность того, что из 6 дней 4 и больше дней будут отработаны с прибылью:

где ,

Используя функцию MS Excel БИНОМ.РАСП, вычислим вероятность того, что из 6 дней не более 3 дней будут завершены с прибылью (значение интегральной величины - 1):

P 6 (≤3 ) = БИНОМ.РАСП(3; 6; 0,61; 1) = 0,435.

Вероятность того, что из 6 дней все будут отработаны с убытками:

Тот же показатель вычислим, используя функцию MS Excel БИНОМ.РАСП:

P 6 (0 ) = БИНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.

Решить задачу самостоятельно, а затем посмотреть решение

Пример 2. В урне 2 белых шара и 3 чёрных. Из урны вынимают шар, устанавливают цвет и кладут обратно. Попытку повторяют 5 раз. Число появления белых шаров - дискретная случайная величина X , распределённая по биномиальному закону. Составить закон распределения случайной величины. Определить моду, математическое ожидание и дисперсию.

Продолжаем решать задачи вместе

Пример 3. Из курьерской службы отправились на объекты n = 5 курьеров. Каждый курьер с вероятностью p = 0,3 независимо от других опаздывает на объект. Дискретная случайная величина X - число опоздавших курьеров. Построить ряд распределения это случайной величины. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение. Найти вероятность того, что на объекты опоздают не менее двух курьеров.

Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:

Биномиальный закон распределения
Пуассоновский закон распределения
Геометрический закон распределения
Гипергеометрический закон распределения

Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.

1. Биномиальный закон распределения.

Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$. Фактически, случайная величина $X$ - это число появлений события $A$ в $n$ независимых испытаний . Закон распределения вероятностей случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end{array}$

Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.

Пример . В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ - числа мальчиков в семье.

Пусть случайная величина $\xi $ - число мальчиков в семье. Значения, которые может принимать $\xi:\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$, где $n=2$ - число независимых испытаний, $p=0,5$ - вероятность появления события в серии из $n$ испытаний. Получаем:

$P\left(\xi =0\right)=C^0_2\cdot {0,5}^0\cdot {\left(1-0,5\right)}^{2-0}={0,5}^2=0,25;$

$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot {\left(1-0,5\right)}^{2-1}=2\cdot 0,5\cdot 0,5=0,5;$

$P\left(\xi =2\right)=C^2_2\cdot {0,5}^2\cdot {\left(1-0,5\right)}^{2-2}={0,5}^2=0,25.$

Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:

$\begin{array}{|c|c|}
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end{array}$

Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _{i=1}^{n}P(\xi _{{\rm i}})=0,25+0,5+0,25=1 $.

Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt{D\left(\xi \right)}=\sqrt{0,5}\approx 0,707$.

2. Закон распределения Пуассона.

Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.

Замечание . Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.

Пример . Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.

Пример . Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.

Пусть дискретная случайная величина $X$ - число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.

$P\left(X=0\right)={{1^0}\over {0!}}\cdot e^{-1}=0,368;$

$P\left(X=1\right)={{1^1}\over {1!}}\cdot e^{-1}=0,368;$

$P\left(X=2\right)={{1^2}\over {2!}}\cdot e^{-1}=0,184;$

$P\left(X=3\right)={{1^3}\over {3!}}\cdot e^{-1}=0,061;$

$P\left(X=4\right)={{1^4}\over {4!}}\cdot e^{-1}=0,015;$

$P\left(X=5\right)={{1^5}\over {5!}}\cdot e^{-1}=0,003;$

$P\left(X=6\right)={{1^6}\over {6!}}\cdot e^{-1}=0,001;$

$P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$

Закон распределения случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & {{{\lambda }^k}\over {k!}}\cdot e^{-\lambda } \\
\hline
\end{array}$

Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.

3. Геометрический закон распределения.

Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p{\left(1-p\right)}^{k-1},\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.

Пример . Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.

Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.

Пример . На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.

Пусть случайная величина $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^{k-1}$, где: $p=2/5$ - вероятность задержания рыбы через шлюз, $q=1-p=3/5$ - вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.

$P\left(X=1\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^0={{2}\over {5}}=0,4;$

$P\left(X=2\right)={{2}\over {5}}\cdot {{3}\over {5}}={{6}\over {25}}=0,24;$

$P\left(X=3\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^2={{2}\over {5}}\cdot {{9}\over {25}}={{18}\over {125}}=0,144;$

$P\left(X=4\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^3+{\left({{3}\over {5}}\right)}^4={{27}\over {125}}=0,216.$

$\begin{array}{|c|c|}
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end{array}$

Математическое ожидание:

$M\left(X\right)=\sum^n_{i=1}{x_ip_i}=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$

Дисперсия:

$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2=}0,4\cdot {\left(1-2,176\right)}^2+0,24\cdot {\left(2-2,176\right)}^2+0,144\cdot {\left(3-2,176\right)}^2+$

$+\ 0,216\cdot {\left(4-2,176\right)}^2\approx 1,377.$

Среднее квадратическое отклонение:

$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{1,377}\approx 1,173.$

4. Гипергеометрический закон распределения.

Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ - число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:

$P\left(X=k\right)={{C^k_mC^{n-k}_{N-m}}\over {C^n_N}}$

Замечание . Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.

$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК . Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.

Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}$.

Пример . В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.

а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;

б) Найдите числовые характеристики этого распределения.

Пусть случайная величина $X$ - число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ - размер совокупности, $m=5$ - число успехов в совокупности, $n=3$ - размер выборки, $k=0,\ 1,\ 2,\ 3$ - число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)={C_{m}^{k} \cdot C_{N-m}^{n-k} \over C_{N}^{n} } $. Имеем:

$P\left(X=0\right)={{C^0_5\cdot C^3_3}\over {C^3_8}}={{1}\over {56}}\approx 0,018;$

$P\left(X=1\right)={{C^1_5\cdot C^2_3}\over {C^3_8}}={{15}\over {56}}\approx 0,268;$

$P\left(X=2\right)={{C^2_5\cdot C^1_3}\over {C^3_8}}={{15}\over {28}}\approx 0,536;$

$P\left(X=3\right)={{C^3_5\cdot C^0_3}\over {C^3_8}}={{5}\over {28}}\approx 0,179.$

Тогда ряд распределения случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end{array}$

Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.

$M\left(X\right)={{nm}\over {N}}={{3\cdot 5}\over {8}}={{15}\over {8}}=1,875.$

$D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}={{3\cdot 5\cdot \left(1-{{5}\over {8}}\right)\cdot \left(1-{{3}\over {8}}\right)}\over {8-1}}={{225}\over {448}}\approx 0,502.$

$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{0,502}\approx 0,7085.$

Распределения вероятностей дискретных случайных величин. Биномиальное распределение. Распределение Пуассона. Геометрическое распределение. Производящая функция.

6. Распределения вероятностей дискретных случайных величин

6.1. Биномиальное распределение

Пусть производится n независимых испытаний, в каждом из которых событие A может либо появится, либо не появится. Вероятность p появления события A во всех испытаниях постоянна и не изменяется от испытания к испытанию. Рассмотрим в качестве случайной величины X число появлений события A в этих испытаниях. Формула, позволяющая найти вероятность появления события A ровно k раз в n испытаниях, как известно, описывается формулой Бернулли

Распределение вероятностей, определяемое формулой Бернулли, называется биномиальным .

Этот закон назван "биномиальным" потому, что правую часть можно рассматривать как общий член разложения бинома Ньютона

Запишем биномиальный закон в виде таблицы


	p n	np n –1 q				q n

Найдем числовые характеристики этого распределения.

По определению математического ожидания для ДСВ имеем

Запишем равенство, являющееся бином Ньютона

и продифференцируем его по p. В результате получим

Умножим левую и правую часть на p :

Учитывая, что p + q =1, имеем

(6.2)

Итак, математическое ожидание числа появлений событий в n независимых испытаниях равно произведению числа испытаний n на вероятность p появления события в каждом испытании .

Дисперсию вычислим по формуле

Для этого найдем

Предварительно продифференцируем формулу бинома Ньютона два раза по p :

и умножим обе части равенства на p 2:

Следовательно,

Итак, дисперсия биномиального распределения равна

. (6.3)

Данные результаты можно получить и из чисто качественных рассуждений. Общее число X появлений события A во всех испытаниях складываются из числа появлений события в отдельных испытаниях. Поэтому если X 1 – число появлений события в первом испытании, X 2 – во втором и т.д., то общее число появлений события A во всех испытаниях равно X=X 1 +X 2 +…+X n . По свойству математического ожидания:

Каждое из слагаемых правой части равенства есть математическое ожидание числа событий в одном испытании, которое равно вероятности события. Таким образом,

По свойству дисперсии:

Так как , а математическое ожидание случайной величины, которое может принимать только два значения, а именно 1 2 с вероятностью p и 0 2 с вероятностью q , то
. Таким образом,
В результате, получаем

Воспользовавшись понятием начальных и центральных моментов, можно получить формулы для асимметрии и эксцесса:

. (6.4)

Рис. 6.1

Многоугольник биномиального распределения имеет следующий вид (см. рис. 6.1). ВероятностьP n (k ) сначала возрастает при увеличении k , достигает наибольшего значения и далее начинает убывать. Биномиальное распределение асимметрично, за исключением случая p =0,5. Отметим, что при большом числе испытаний n биномиальное распределение весьма близко к нормальному. (Обоснование этого предложения связано с локальной теоремой Муавра-Лапласа.)

Число m 0 наступлений события называется наивероятнейшим , если вероятность наступления события данное число раз в этой серии испытаний наибольшая (максимум в многоугольнике распределения) . Для биномиального распределения

Замечание. Данное неравенство можно доказать, используя рекуррентную формулу для биномиальных вероятностей:

(6.6)

Пример 6.1. Доля изделий высшего сорта на данном предприятии составляет 31%. Чему равно математического ожидание и дисперсия, также наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий?

Решение. Поскольку p =0,31, q =0,69, n =75, то

M[X ] = np = 750,31 = 23,25; D[X ] = npq = 750,310,69 = 16,04.

Для нахождения наивероятнейшего числа m 0 , составим двойное неравенство

Отсюда следует, что m 0 = 23.

Теория вероятности незримо присутствует в нашей жизни. Мы не обращаем на это внимания, но каждое событие в нашей жизни имеет ту или иную вероятность. Принимая во внимание огромное количество вариантов развития событий, нам становится необходимым определять наиболее вероятные и наименее вероятные из них. Наиболее удобно анализировать такие вероятностные данные графически. В этом нам может помочь распределение. Биномиальное - одно из самых лёгких и самых точных.

Прежде чем перейти непосредственно к математике и теории вероятности, разберёмся с тем, кто же первый придумал такой вид распределения и какова история развития математического аппарата для этого понятия.

История

Понятие вероятности известно ещё с древних времён. Однако древние математики не придавали ей особо значения и смогли заложить только основы для теории, ставшей впоследствии теорией вероятности. Они создали некоторые комбинаторные методы, которые сильно помогли тем, кто позже создал и развил саму теорию.

Во второй половине семнадцатого века началось формирование основных понятий и методов теории вероятности. Были введены определения случайных величин, способы вычисления вероятности простых и некоторых сложных независимых и зависимых событий. Продиктован такой интерес к случайным величинам и вероятностям был азартными играми: каждый человек хотел знать, какие у него шансы победить в игре.

Следующим этапом стало применение в теории вероятности методов математического анализа. Этим занялись видные математики, такие как Лаплас, Гаусс, Пуассон и Бернулли. Именно они продвинули эту область математики на новый уровень. Именно Джеймс Бернулли открыл биномиальный закон распределения. Кстати, как мы позже выясним, на основе этого открытия были сделаны ещё несколько, которые позволили создать закон нормального распределения и ещё множество других.

Сейчас, прежде чем начать описывать распределение биномиальное, мы немного освежим в памяти понятия теории вероятностей, наверняка уже забытые со школьной скамьи.

Основы теории вероятностей

Будем рассматривать такие системы, в результате действия которых возможны только два исхода: "успех" и "не успех". Это легко понять на примере: мы подбрасываем монетку, загадав то, что выпадет решка. Вероятности каждого из возможных событий (выпадет решка - "успех", выпадет орёл - "не успех") равны 50 процентам при идеальной балансировке монеты и отсутствии прочих факторов, которые могут повлиять на эксперимент.

Это было самое простое событие. Но бывают ещё и сложные системы, в которых выполняются последовательные действия, и вероятности исходов этих действий будут различаться. Например, рассмотрим такую систему: в коробке, содержимое которой мы не можем разглядеть, лежат шесть абсолютно одинаковых шариков, три пары синего, красного и белого цветов. Мы должны достать наугад несколько шариков. Соответственно, вытащив первым один из белых шариков, мы уменьшим в разы вероятность того, что следующим нам тоже попадётся белый шарик. Происходит это потому, что меняется количество объектов в системе.

В следующем разделе рассмотрим более сложные математические понятия, вплотную подводящие нас к тому, что означают слова "нормальное распределение", "биномиальное распределение" и тому подобные.

Элементы математической статистики

В статистике, которая является одной из областей применения теории вероятностей, существует множество примеров, когда данные для анализа даны не в явном виде. То есть не в численном, а в виде разделения по признакам, например, по половым. Для того чтобы применить к таким данным математический аппарат и сделать из полученных результатов какие-то выводы, требуется перевести исходные данные в числовой формат. Как правило, для осуществления этого положительному исходу присваивают значение 1, а отрицательному - 0. Таким образом, мы получаем статистические данные, которые можно подвергнуть анализу с помощью математических методов.

Следующий шаг в понимании того, что такое биномиальное распределение случайной величины, - это определение дисперсии случайной величины и математического ожидания. Об этом поговорим в следующем разделе.

Математическое ожидание

На самом деле понять то, что такое математическое ожидание, несложно. Рассмотрим систему, в которой существует много разных событий со своими различными вероятностями. Математическим ожиданием будет называться величина, равная сумме произведений значений этих событий (а математическом виде, о котором мы говорили в прошлом разделе) на вероятности их осуществления.

Математическое ожидание биномиального распределения рассчитывается по той же самой схеме: мы берём значение случайной величины, умножаем его на вероятность положительного исхода, а затем суммируем полученные данные для всех величин. Очень удобно представить эти данные графически - так лучше воспринимается разница между математическими ожиданиями разных величин.

В следующем разделе мы расскажем вам немного о другом понятии - дисперсии случайной величины. Оно тоже тесно связано с таким понятием, как биномиальное распределение вероятностей, и является его характеристикой.

Дисперсия биномиального распределения

Эта величина тесно связана с предыдущей и также характеризует распределение статистических данных. Она представляет собой средний квадрат отклонений значений от их математического ожидания. То есть дисперсия случайной величины - это сумма квадратов разностей между значением случайной величины и её математическим ожиданием, умноженная на вероятность этого события.

В общем, это всё, что нам нужно знать о дисперсии для понимания того, что такое биномиальное распределение вероятностей. Теперь перейдём непосредственно к нашей основной теме. А именно к тому, что же кроется за таким на вид достаточно сложным словосочетанием "биномиальный закон распределения".

Биномиальное распределение

Разберёмся для начала, почему же это распределение биномиальное. Оно происходит от слова "бином". Может быть, вы слышали о биноме Ньютона - такой формуле, с помощью которой можно разложить сумму двух любых чисел a и b в любой неотрицательной степени n.

Как вы, наверное, уже догадались, формула бинома Ньютона и формула биномиального распределения - это практически одинаковые формулы. За тем лишь исключением, что вторая имеет прикладное значение для конкретных величин, а первая - лишь общий математический инструмент, применения которого на практике могут быть различны.

Формулы распределения

Функция биномиального распределения может быть записана в виде суммы следующих членов:

(n!/(n-k)!k!)*p k *q n-k

Здесь n - число независимых случайных экспериментов, p- число удачных исходов, q- число неудачных исходов, k - номер эксперимента (может принимать значения от 0 до n),! - обозначение факториала, такой функции числа, значение которой равно произведению всех идущих до неё чисел (например, для числа 4: 4!=1*2*3*4=24).

Помимо этого, функция биномиального распределения может быть записана в виде неполной бета-функции. Однако это уже более сложное определение, которое используется только при решении сложных статистических задач.

Биномиальное распределение, примеры которого мы рассмотрели выше, - одно из самых простых видов распределений в теории вероятностей. Существует также нормальное распределение, являющееся одним из видов биномиального. Оно используется чаще всего, и наиболее просто в расчётах. Бывает также распределение Бернулли, распределение Пуассона, условное распределение. Все они характеризуют графически области вероятности того или иного процесса при разных условиях.

В следующем разделе рассмотрим аспекты, касающиеся применения этого математического аппарата в реальной жизни. На первый взгляд, конечно, кажется, что это очередная математическая штука, которая, как обычно, не находит применения в реальной жизни, и вообще не нужна никому, кроме самих математиков. Однако это далеко не так. Ведь все виды распределений и их графические представления были созданы исключительно под практические цели, а не в качестве прихоти учёных.

Применение

Безусловно, самое важное применение распределения находят в статистике, ведь там нужен комплексный анализ множества данных. Как показывает практика, очень многие массивы данных имеют примерно одинаковые распределения величин: критические области очень низких и очень высоких величин, как правило, содержат меньше элементов, чем средние значения.

Анализ больших массивов данных требуется не только в статистике. Он незаменим, например, в физической химии. В этой науке он используется для определения многих величин, которые связаны со случайными колебаниями и перемещениями атомов и молекул.

В следующем разделе разберёмся, насколько важно применение таких статистических понятий, как биномиальное распределение случайной величины в повседневной жизни для нас с вами.

Зачем мне это нужно?

Многие задают себе такой вопрос, когда дело касается математики. А между прочим, математика не зря называется царицей наук. Она является основой физики, химии, биологии, экономики, и в каждой из этих наук применяется в том числе и какое-либо распределение: будь это дискретное биномиальное распределение, или же нормальное, не важно. И если мы получше присмотримся к окружающему миру, то увидим, что математика применяется везде: в повседневной жизни, на работе, да даже человеческие отношения можно представить в виде статистических данных и провести их анализ (так, кстати, и делают те, кто работают в специальных организациях, занимающихся сбором информации).

Сейчас поговорим немного о том, что же делать, если вам нужно знать по данной теме намного больше, чем то, что мы изложили в этой статье.

Та информация, что мы дали в этой статье, далеко не полная. Существует множество нюансов, касаемо того, какую форму может принимать распределение. Биномиальное распределение, как мы уже выяснили, является одним из основных видов, на котором зиждется вся математическая статистика и теория вероятностей.

Если вам стало интересно, или в связи с вашей работой вам нужно знать по этой теме гораздо больше, нужно будет изучить специализированную литературу. Начать следует с университетского курса математического анализа и дойти там до раздела теории вероятностей. Также пригодятся знания в области рядов, ведь биномиальное распределение вероятностей - это ни что иное, как ряд последовательных членов.

Заключение

Прежде чем закончить статью, мы хотели бы рассказать ещё одну интересную вещь. Она касается непосредственно темы нашей статьи и всей математики в целом.

Многие люди твердят, что математика - бесполезная наука, и ничто из того, что они проходили в школе, им не пригодилось. Но знание ведь никогда не бывает лишним, и если вам что-то не пригодилось в жизни, значит, вы просто этого не помните. Если у вас есть знания, они могут вам помочь, но если их нет, то и помощи от них ждать не приходится.

Итак, мы рассмотрели понятие биномиального распределения и все связанные с ним определения и поговорили о том, как же это применяется в нашей с вами жизни.