Как найти сечение круга. Площадь круга в задаче B5
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
![]()
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R
= 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .

Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R
= 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.
Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях - это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:

В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга - площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC - прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S /π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи - самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
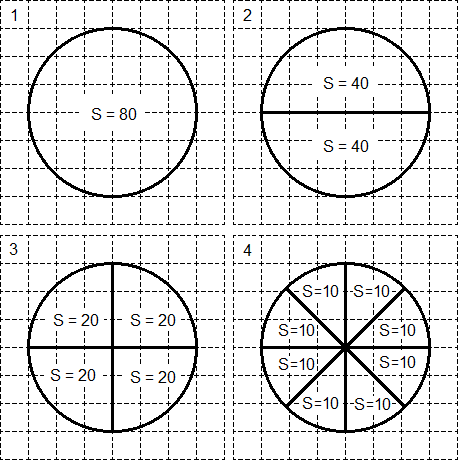
Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам - получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два - получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S круга = 240, то «ошметки» имеют площадь S = 240: 8 = 30;
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов - каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.

Как нам известно из школьной программы, кругом принято называть плоскую геометрическую фигуру, которая состоит из множества точек, равноудалённых от центра фигуры. Так как все они находятся на одинаковом расстоянии, они формируют окружность.
Удобная навигация по статье: